Mouvements périodiques et astronomie
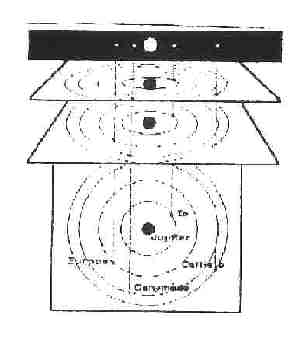
Jupiter est souvent très bien visible dans le ciel du soir . Aux jumelles (grossissement 8 à 10), en se stabilisant, on peut voir les satellites les plus gros de Jupiter (Io, Europe, Ganymède et Callisto).
En photographiant régulièrement ces satellites, on peut déterminer le rayon de l’orbite de chaque satellite autour de Jupiter et leur période de rotation (on admet que le mouvement autour de Jupiter est circulaire)
La Terre, notre lieu d’observation, est pratiquement située dans le plan de leurs orbites, ce qui fait paraitre celles-ci comme "rectilignes".

Les photographies jointes ont été réalisées pendant plusieurs mois par l’astronome Culver aux USA, ce qui explique que certaines aient pu être prises à midi (les heures sont données en temps universel .. et il peut être midi à Greenwich alors qu’il fait encore nuit dans certaines régions des USA)
Cliquez sur l'image
On se propose de déterminer successivement le rayon a de l’orbite de chaque satellite, puis sa période de révolution.
Pour nous permettre de travailler plus commodément, ces satellites ont été partiellement identifiés par un chiffre (1 pour Io, 2 pour Europe, 3 pour Ganymède et 4 pour Callisto. Pour simplifier, on ne travaillera donc que sur les points ainsi identifiés
Détermination du rayon de l’orbite d’un satellite
La distance apparente de Jupiter au satellite choisi va se mesurer en minutes d’arc.
L’échelle de la photographie est telle qu’une distance de 1 cm mesurée sur la photographie correspond à
2/1,1 = 1,82 ' d’arc
A/ Choisir un des 4 satellites
B/Mesurer au double décimètre la distance séparant le satellite au centre de Jupiter selon la date de la photo. Reporter les résultats dans un tableau

C/Sur du papier millimétré, placer les points permettant de tracer la courbe représentant les variations de la distance apparente du satellite de Jupiter en fonction du temps
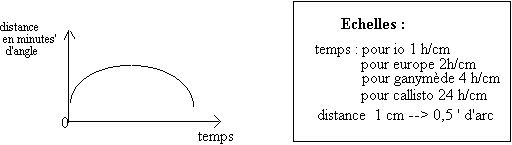
D/Tracer la courbe avec le plus de soin possible (la courbe doit être régulière et ne passera peut-être pas par tous les points)
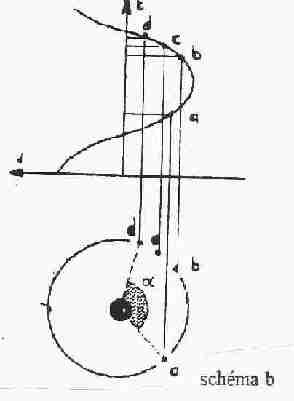
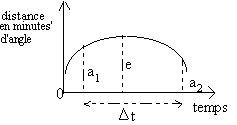
E/En regardant le schéma b ci-dessous, vous comprendrez que la distance associée au point le plus haut de la courbe (extrémum) correspond au rayon a de l’orbite du satellite.
Indiquer ce rayon en minutes d’arc pour le satellite étudié
a = ........... ' d’arc
F/ Pour en déduire le rayon en km, il faut effectuer un "petit" calcul.
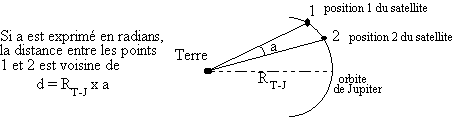
*Comment exprimer a en radians ?
correspondance degré-radians : 360° = 2p rad
donc, 1° = 2p / 360 rad
1° = 60 ‘ d’arc donc 1 ‘ d’arc = 2p / 360x60 rad
donc a rad = a x 2p / 360 x 60 = ................... rad
Au moment des photographies, la distance Terre-Jupiter (R T-J) était de 4,46 UA (1 UA = 150 000 000 km)
*En déduire la distance d (en UA puis en km)
d = a rad x R T-J = ...................... ......................
Période
La période du satellite correspond au temps qu’il met pour faire le tour de Jupiter. On peut également la déterminer à l’aide des photographies.
En regardant le schéma b, vous comprendrez qu’en faisant un schéma à l’échelle, il vous est possible de déterminer l’angle a, de savoir le temps mis par le satellite pour décrire cet angle et d’en déduire la période du satellite.
1/ Tracez un cercle de rayon égal à l’extrèmum e mesuré sur la courbe tracée précédemment
2/Repérez sur la courbe 2 points de chaque côté de l’extrémum
3/En mesurant, placez sur le cercle le point correspondant à a1 et (de l’autre côté du rayon JE) le point correspondant à a2. Joindre 1 et 2 au centre J du cercle
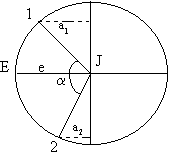
Vous pouvez alors, avec un rapporteur, mesurer l’angle a (en degrés) balayé par le satellite pour aller de 1 à 2.
a = ......... °
4/ Détermination de la période
*sur la courbe, déterminez l’intervalle de temps Dt séparant les passages aux positions 1 et 2.
Dt = ........... h (attention aux jours qui font 24 heures)
*une période correspond à un tour soit 360°. La période de rotation du satellite sera donc
T = Dt x 360 / a = .............. heures
d’après "Les cahiers du CLEA"